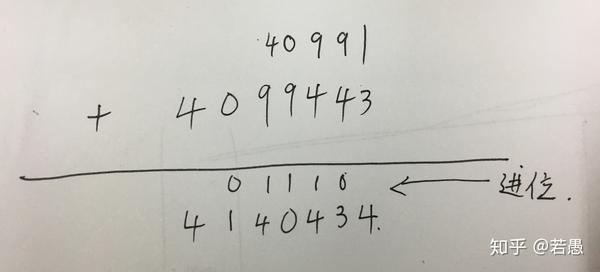有趣的大数运算

出一个有趣并且有意义的题目：50的阶乘是多少？ 100的阶乘是多少？400的阶乘是多少？如果有一台超级计算机，任意长度数字的阶乘如何计算？

答案2天后公布，有兴趣的小伙伴可在回复区讨论方案，最好给出确切代码

ps: 400的阶乘答案如下，用于对照验证，macbook pro 使用chrome计算用时小于1s

64034522846623895262347970319503005850702583026002959458684445942802397169186831436278478647463264676294350575035856810848298162883517435228961988646802997937341654150838162426461942352307046244325015114448670890662773914918117331955996440709549671345290477020322434911210797593280795101545372667251627877890009349763765710326350331533965349868386831339352024373788157786791506311858702618270169819740062983025308591298346162272304558339520759611505302236086810433297255194852674432232438669948422404232599805551610635942376961399231917134063858996537970147827206606320217379472010321356624613809077942304597360699567595836096158715129913822286578579549361617654480453222007825818400848436415591229454275384803558374518022675900061399560145595206127211192918105032491008000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

11.5更新：

JavaScript 中最大的安全整数是 -(2\^{53}-1)\~ 2\^{53}-1 ，即: -9007199254740991 \~ 9007199254740991。换句话说，整数超过这个范围就会丢失精度，那超过这个范围的基本运算也别指望有多精确了。那怎么办？难道因为这个问题月球就不去了？火星不探测了？要知道美国阿波罗登月的时候还是计算机还是电子管。

我们可以换一种思路，用字符串表示数字，比如 "9007199254740999"，不存在四舍五入精度丢失的问题，这样不管数值多大都没影响。用数字表示字符串之后，那么数字的运算就转换成字符串的运算。首先，我们研究一下最基本的“加法”运算。

先从需求入手，假设我们需要一个 add 方法，能实现两个字符串类型的“整数”的“加法”运算，得到数值相加后的字符串：

let num1 = "9007199254740991"
let num2 = "1229007199254740993443"
add(num1, num2)  // "1229016206453995734434"

ps：在浏览器空控制台输入：9007199254740991+1229007199254740993443 ，你会得到结果：1.2290162064539957e+21 ，和我们的需求相比精度丢失很多位。

回想一下小学的课本，如何手写加法运算

从最后一个数字开始向前逐一相加逢10进1，下一位数字相加的时候加上次计算的进位。我们可以把这个逻辑运用到字符串运算中。

function add(num1, num2) {
 let len = Math.max(num1.length, num2.length)
 num1 = num1.padStart(len, 0)
 num2 = num2.padStart(len, 0)
 let flag = 0
 let result = ''
 let temp = 0
 for(let i=len-1; i>=0; i--){
   temp = flag + parseInt(num1[i]) + parseInt(num2[i])
   result = (temp%10) + result 
   flag = parseInt(temp/10)
 }
 result = (flag===1?'1':'') + result
 return result
}
 
let num1 = "9007199254740991"
let num2 = "1229007199254740993443"
add(num1, num2)  // "1229016206453995734434"

这里我们对数字进行了填充变成等长，方便逐位计算。(当然上面的函数可以继续优化，比如一个很长的数字加1，进行等长填充，逐位计算并不是好的方式)

减法的实现原理类似，区别是“借位”而不是“进位”。当然对于减法我们需要考虑到结果为负的情况。

function sub(num1, num2) {
  if(num1 === num2) return '0'
  let isMinus = false
  if(lt(num1, num2)) {
    [num1, num2] = [num2, num1]
    isMinus = true
  }
 
  let len = Math.max(num1.length, num2.length)
  num1 = num1.padStart(len, 0)
  num2 = num2.padStart(len, 0)
 
  let flag = 0,
      result = '',
      temp
  for(let i=len-1; i>=0; i--) {
     temp = parseInt(num1[i]) - flag -parseInt(num2[i]) 
     if(temp < 0) {
       result = (10 + temp) + result
       flag = 1
     }else {
       result = temp + result 
       flag = 0
     }
  }
  result = (isMinus?'-':'') + result.replace(/^0+/, '') //去掉前面多余的0，如"1324"-"1315"
  return result
}
 
let num1 = "9007199254740991"
let num2 = "1229007199254740993443"
sub(num1, num2)  // "-1228998192055486252452"

上面的代码中我们用到了lt 方法用于比较两个数字的大小。(千万不要把字符串转换成数字直接比较大小)

function lt(num1, num2) {
  if(num1.length < num2.length) {
    return true
  } else if(num1.length === num2.length) {
    return num1 < num2
  } else {
    return false
  }
}

乘法的实现逻辑上比加法减法要复杂，但乘法可以分解为简单乘法和加法。比如对于"2018"乘以"21"，等价于

mul("2018", "21")  //等价于
add( mul("2018", "1") , mul("2018", "2") + "0"）
 
mul("2018", "201") //等价于
add(add(mul("2018", "1") , mul("2018", "2") + "0"）, mul("2018", "2") + "00")

所以我们只需要会计算一个长数字字符串和一个单字符数字的乘积就行，和加法类似，逐位相乘，只不过不是进"1"，而是进"n"。

以下是完整代码

function mul(num1, num2) {
  if(num1 === '0' || num2 === '0') return '0'
  let flag = 0,
      result = '0',
      tempResult = '',
      temp = 0
  for(let i=num2.length-1; i>=0; i--) {
    flag = 0
    tempResult = ''
    temp = 0
    for(let j=num1.length-1; j>=0; j--) {
      temp = parseInt(num2[i])*parseInt(num1[j]) + flag
      tempResult = (temp%10) + tempResult
      flag = parseInt(temp/10)
    }
    tempResult = (flag>0?flag:'') + tempResult
    result = add(result, tempResult+'0'.repeat(num2.length-1-i))
  }
  return result
}
 
let num1 = "9007199254740991"
let num2 = "1229007199254740993443"
mul(num1, num2) //"11069912729198615705685978274994322013"

有了加法和乘法，阶乘的运算就简单的多了。

6! //等价于
6*5*4*3*2*1

我们先用原始的方法实现阶乘

function fact(num) {
  let result = 1
  for(let i=1; i<=num; i++){
    result = result * i
  }
  return result
}

改造一下即可

function fact(num) {
  let result = '1'
  for(let i='1'; lte(i, num); i=add(i, '1')){
    result = mul(result, i)
  }
  return result
}
 
function lte(num1, num2) {
  if(num1.length < num2.length) {
    return true
  } else if(num1.length === num2.length) {
    return num1 <= num2
  } else {
    return false
  }
}
 
fact('400') //计算出400的阶乘

至此，我们运用js的基础知识解决了世纪难题，用计算器计算登月轨道成为可能。有兴趣的小伙伴也可以试着实现字符串数字的除法运算，嗯，貌似挺复杂。

饥人谷一直致力于培养有灵魂的编程者，打造专业有爱的国内前端技术圈子。如造梦师一般帮助近千名不甘寂寞的追梦人把编程梦变为现实，他们以饥人谷为起点，足迹遍布包括facebook、阿里巴巴、百度、网易、京东、今日头条、大众美团、饿了么、ofo在内的国内外大小企业。了解培训课程：加微信 xiedaimala03，官网:https://jirengu.com

本文作者：饥人谷若愚老师

目录

有趣的大数运算